AnotherDilbert
SOC-14 5K
1. explain without shouting what we actually draw on the game board according to the rules.
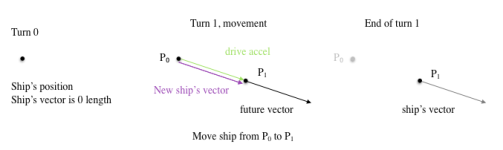
This is an example play surface:
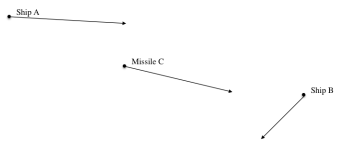
It shows the positions and velocity vectors of two ships and a missile.
The distance between the objects can be determined by measurement with a ruler.
The points, the origins of the velocity vectors, shows the position of the ships.2. if the "vectors" are velocity vectors then you do not know the positions of ships
No, the vectors shows the speed and direction of travel, from the position they currently occupy.3. if the "vectors" show position - which they must to allow for weapon range- then they are displacement.
Each ship or other object has a position, represented by a miniature or marker:
Each ship has a vector, showing it's velocity:LBB2'81, p26:
4. Units: Starships and space vehicles are individually represented by spacecraft miniatures, or (if necessary) by counters or markers. Because spacecraft miniatures are almost certainly oversize for the scale in use, each should be marked with a spot or point to designate the exact true location of the ships in play.
We change the velocity vector with acceleration vectors:LBB2'81, p27:
Each ship has a vector, which expresses that ship's velocity as a line (arrow) o f a specific direction.
LBB2'81, p26:
3. Thrust: Maneuver drive thrust is measured in Gs (gravities) expressed as a vector of both length and direction.
https://www.britannica.com/science/vector-physicsDistance and direction - a displacement vector.
Not force, not acceleration, not momentum, not velocity - direction and distance is displacement. QED
vector, in physics, a quantity that has both magnitude and direction. It is typically represented by an arrow whose direction is the same as that of the quantity and whose length is proportional to the quantity’s magnitude.
https://www.britannica.com/science/velocityFor example, displacement, velocity, and acceleration are vector quantities, while speed (the magnitude of velocity), time, and mass are scalars.
velocity, quantity that designates how fast and in what direction a point is moving.
https://en.wikipedia.org/wiki/Vector_(mathematics_and_physics)
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector[1] or spatial vector[2]) is a geometric object that has magnitude (or length) and direction.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors.[7] Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow.
https://physics.ucf.edu/~roldan/classes/phy2048-ch3_sp12.pdf

A vector is something with a direction and magnitude (length).
Displacement, velocity, and acceleration can all be described as vectors.
Note that the very next sentence proves the authors didn't understand the physics of it since they then say.
Last edited by a moderator: