mike wightman
SOC-14 10K
<clap> <clap> so you take something out of context for a GOTCHA. Pathetic.Wikipedia Link: Whataboutism
The rest of the post show that this is intended as a rhetorical question.
<clap> <clap> so you take something out of context for a GOTCHA. Pathetic.Wikipedia Link: Whataboutism
There is no resulting vector, no total acceleration.A ship on the ground has no vector because it is not moving and has no potential to move in the future because the resultant force on the ship is zero. There is no vector to draw.
The "vectors" that you are plotting are not "vectors" they are forces, the resultant of which is then applied to the current vector in order to determine future position.
Make your mind up?Vectors in LBB2 are not force arrows they are displacement arrows, ...
Yes, force vectors that causes acceleration (F = ma), that integrated over the turn is a velocity vector showing distance travelled per turn. Does that make any difference whatsoever to LBB2 RAW?
Displacement per turn, a velocity...Vector movement in Traveller has you drawing displacement vectors, not force vectors.
Addition is commutative and associative, the result is trivially the same vector either way.Yes it makes a difference because the final displacement "vector" that is actually drawn on the surface does not represent force, or energy, or velocity. It shows displacement only.
The rules specify aerobraking, but not lift, yes. Presumably spacecraft doesn't have enough lift to significantly influence the outcome, as their shapes would suggest.So aerobraking exists because the rules say so, but lift doesn't?
You are assuming lift is enough, not I.So in level flight lift and weight cancel out yes? And if you apply a 1g continuous thrust to an object with balanced forces what happens?
The forces balance, there is no resultant force, so no vector is drawnThere is no resulting vector, no total acceleration.
The forces operating on the craft, like gravity, are always there.
It is not weightless.
I am saying that you keep plotting "force vectors" where the game requires the plotting of "displacement vectors"Make your mind up?
YesYes,
It is be we do not track velocity we track displacementDisplacement per turn, a velocity...
Yes 100mm-25mm-50mm=25mmAddition is commutative and associative, the result is trivially the same vector either way.
I agree, but it would add complication that may not be worth the effortThe rules specify aerobraking, but not lift, yes. Presumably spacecraft doesn't have enough lift to significantly influence the outcome, as their shapes would suggest.
Aerobraking is also a vast simplification, it is e.g. not proportional to speed.
Yes I amYou are assuming lift is enough, not I.
Yes, you are still wrong. I used LBB2'77 as specified by the OP earlier. It uses Imperial measurements.Still wrong
Gravity does not operate on the ship's acceleration, but the ship's position.The thrust vector should be plotted to a position 100mm above the planet surface, the midpoint of which places it in the 0.5g band of all planet sizes 8-10.
Gravity is not optional. It is always on. The acceleration always act on the spacecraft. The acceleration vector is always added.The forces balance, there is no resultant force, so no vector is drawn
The "displacement" is displacement per turn = distance per time = velocity.I am saying that you keep plotting "force vectors" where the game requires the plotting of "displacement vectors"
...
It is be we do not track velocity we track displacement
Agreed.I agree, but it would add complication that may not be worth the effort

Change the vector, then when all changes to vector are done, change the position of the ship.In a player’s movement phase, he will indicate the acceleration (new vector) he wishes to apply, and note any gravitational influence vector he is required to apply,and then add them to his ship’s present vector. His ship then moves in the direction of its new vector, for the length of the vector. The vector then remains on the playing surface for reference during the next applicable movement phase.
It shouldn't matter if I move from 77 to 81, but if we work in inches it is the same result.Yes, you are still wrong. I used LBB2'77 as specified by the OP earlier. It uses Imperial measurements.
Yes, the half way point of the maneuver vector is affected by the gravity band it is in, which is the 0.5g band.Gravity does not operate on the ship's acceleration, but the ship's position.
All the accelerations add together to change the velocity vector.
NoTurn 1: Position [0,0] Velocity vector [0,0]: midpoint of the velocity vector is [0,0] on the planets surface (in the 1.125 G band).
Accelerate upwards by 1 G during the entire turn, add 100 mm upwards.
Gravity accelerates downwards by 1.125 G (the size 9 world used earlier) during the entire turn add 112.5 mm downwards.
Total acceleration downwards 0.125 G (12.5 mm), or in other words "the vehicle cannot move".
This is not the rules as writtenLet's try accelerating upwards again.
We start on the planet's surface, position [0,0].
We have no velocity, the (velocity) vector is [0,0].
Turn 1: Movement phase:
In a player’s movement phase, he will indicate the acceleration (new vector) he wishes to apply, and note any gravitational influence vector he is required to apply, and then add them to his ship’s present vector.
(1) We accelerate upwards by 1 G: Draw an (acceleration) vector [+100 mm,0] at the end of the (velocity) vector without moving the ship.
(2) The (velocity) vector start at position [0,0] in the direction [0,0], midpoint [0,0] on the planets surface in the 1.125 G band. Add an (acceleration) vector [-112.5 mm, 0] to the end of the other acceleration vector.
Nope. the ship's movement plot is 100mm up.(3) If there are no other accelerations, add the accelerations to the velocity vector. The new velocity vector is [0,0] + [+100 mm,0] + [-112.5 mm, 0] = [-12.5 mm, 0].
His ship then moves in the direction of its new vector, for the length of the vector. The vector then remains on the playing surface for reference during the next applicable movement phase.
Move the ship from position [0,0] with the velocity vector [-12.5 mm, 0] to position [-12.5 mm, 0] down into the planet, which we can't, so remain in position [0,0].
Or in other words "the vehicle cannot move".
Eh, I'd better draw that...
Then show me why LBB2 and Mayday are wrong?and you are not applying the rules as written the rules as written say
This is wrong?Nope. the ship's movement plot is 100mm up.
Half way up that imaginary line, at 50mm, that puts the ship in the 0.5g gravity band.
So we subtract 50mm and then a further 25mm for air resistance
Total 25mm up.
LBB2'77, p26: In a player’s movement phase, he will indicate the acceleration (new vector) he wishes to apply, and note any gravitational influence vector he is required to apply, and then add them to his ship’s present vector. His ship then moves in the direction of its new vector, for the length of the vector. The vector then remains on the playing surface for reference during the next applicable movement phase.
LBB2'77, p26:
In a player’s movement phase, he will indicate the acceleration (new vector) he wishes to apply, and note any gravitational influence vector he is required to apply, and then add them to his ship’s present vector. His ship then moves in the direction of its new vector, for the length of the vector. The vector then remains on the playing surface for reference during the next applicable movement phase.

?the vector is not force, it is not velocity, it is displacement
LBB2'81, p27:
Each ship has a vector, which expresses that ship's velocity as a line (arrow) of a specific direction.
Hypothetically, if I place a FREE TRADER on a GIANT ROLLER SKATE and apply the VECTORS above to it using the GRAV DRIVE … what will happen?Turn 1:

And it is an error - we are plotting displacement not velocity.?
It was a looong time since I actually read that part of LBB2...
You can answer the question about a FREE TRADER on a GIANT ROLLER SKATE if you want to.Correct. UP is not the "only direction" available ... but it IS the direction you need to go in order to reach orbit from the surface.

Your 1g band between the planet surface and the first gravity circle is the error. A size 10 world only has 1.25g on its surface, as soon as you take off you are on the 1.0g band which is only 9mm thick, above that you have the 0.75g line which is an additional 14mm thick, so we are now into the 0.5g band which is an additional 23mm - you know what I should have done this earlier because the midpoint of the 100mm "vector" is in the 0.25g zone.Let me try this again.
Starting position 0 with Vector 0, none:
View attachment 3586
In a player’s movement phase, he will indicate the acceleration (new vector) he wishes to apply, and note any gravitational influence vector he is required to apply,
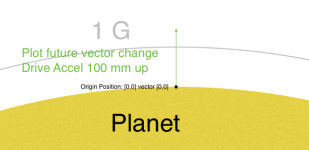
Plot drive acceleration, Vector remains 0, none.
View attachment 3589
The green arrow is not the ship's new Vector, it will soon be added to the Vector.
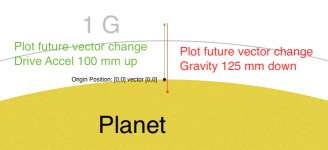
Plot drive gravity, Vector remains 0, none.
View attachment 3588
Neither the green nor the red arrows are part of the ships Vector, they will soon be added.
and then add them to his ship’s present vector.
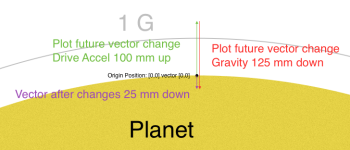
Plot new Vector, add green and red to old Vector 0:
View attachment 3587
Everything is added, the purple arrow is the ship's new Vector.
His ship then moves in the direction of its new vector, for the length of the vector.
Move the ship along the Vector, which fails.
as soon as you take off
LBB2 does not describe this, but in physics the ships would roll along the surface of the planet, keeping the velocity vector tangential to the planet surface, as I discussed a few days ago:Hypothetically, if I place a FREE TRADER on a GIANT ROLLER SKATE and apply the VECTORS above to it using the GRAV DRIVE … what will happen?
Let’s see if we had the same H.S. Physics instructions for “resolving vectors into vertical and horizontal components”.
[EDIT: I better add a disclaimer that this is just a “what if“ and not RAW.]
Let's assume the planet is a perfectly smooth billiard-ball and you can roll on it without friction (leaving RAW and physics far behind):
The length of a line tangential to the planet surface to the 1 G line is about 7½", so you would need a velocity vector of 15" parallel to the surface for the midpoint of the vector to fall outside the 1 G band, freeing you from the shackles of the gravity well (according to LBB2).
You can accelerate at 2" every turn, braked ¼" (⅛ G) by the atmosphere, so resulting 1¾" added velocity per turn. Gravity isn't a factor, as we are supported by the ground (without any friction).
You would need 15" / 1¾" ≈ 9 turns ≈ 1.5 h to achieve that speed.
1.5 h at ⅞ G is... Sorry, I can't be bothered with Imperial units, and as I am not a subject of His Britannic Majesty I have freedom not to.
1.5 h at 0.875 G is a velocity of 1.5 h × 3600 s × 8.75 m/s ≈ 47 250 m/s ≈ 170 000 km/h (~106 000 mph for subjects), travelling a distance of d = at²/2 = 8.75 m/s × 5400² / 2 ≈ 127 500 km.
With a 7000 km world radius, that is a circumference of about 44 000 km.
So, we would need a runway all around the world, and go around it almost three times.
I would call that a slightly problematical approach...
