joshuawood
SOC-3
An interesting and sometimes counterintuitive fact is that population sizes in nature are 30% likely to start with the digit 1. This is called Benford's law (see http://en.wikipedia.org/wiki/Benford's_law ). This law works on the population sizes of countries on Earth (have a look at world population sizes and count how many start with 1 if you don't believe me! You'll see that roughly 30% start with a 1!!!)
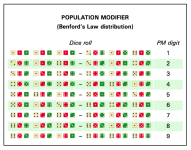
To accurately model a world's population I propose this method. Roll for the world population using the 2 D - 2 method to tell you the exponent of 10 that gives the world population order of magnitude. Then use percentile dice to find out the leading digit:
digit % roll
1 1-30
2 31-48
3 49-60
4 61-70
5 71-78
6 79-85
7 86-92
8 93-97
9 98-00
This method will give you a population with a leading digit roughly in accordance with Benford's law.
For the second digit I propose simply rolling a 10 sided die.
Example 1: I roll 2D-2 and get 6. So I know that the population of the world in the millions. So to find out how many million I roll percentile dice and come up with 72, so the first digit is 5. I roll one ten sided die for the second digit and come up with 9. So the population of this world is 5.9 million.
Example 2: I roll 2D-2 and get 7. So I know that the population of the world in the tens of millions. I roll percentile dice and come up with 51, so the first digit is 3. I roll one ten sided die for the second digit and come up with 3. So the population of this world is 33 million.
Example 3: I roll 2D-2 and get A. So I know the population of the world in the tens of billions. I roll percentile dice and come up with 29, so the first digit is 1. I roll one ten sided die for the second digit and come up with 6. So the population of this world is 16 billion.
I like this method because it is a little bit realistic. Some people might not like using percentile dice to work out the digits. In that case you'd need to assign probabilities using multiple 6 sided dice added together on a bell curve. This would entail a bit more work.
To accurately model a world's population I propose this method. Roll for the world population using the 2 D - 2 method to tell you the exponent of 10 that gives the world population order of magnitude. Then use percentile dice to find out the leading digit:
digit % roll
1 1-30
2 31-48
3 49-60
4 61-70
5 71-78
6 79-85
7 86-92
8 93-97
9 98-00
This method will give you a population with a leading digit roughly in accordance with Benford's law.
For the second digit I propose simply rolling a 10 sided die.
Example 1: I roll 2D-2 and get 6. So I know that the population of the world in the millions. So to find out how many million I roll percentile dice and come up with 72, so the first digit is 5. I roll one ten sided die for the second digit and come up with 9. So the population of this world is 5.9 million.
Example 2: I roll 2D-2 and get 7. So I know that the population of the world in the tens of millions. I roll percentile dice and come up with 51, so the first digit is 3. I roll one ten sided die for the second digit and come up with 3. So the population of this world is 33 million.
Example 3: I roll 2D-2 and get A. So I know the population of the world in the tens of billions. I roll percentile dice and come up with 29, so the first digit is 1. I roll one ten sided die for the second digit and come up with 6. So the population of this world is 16 billion.
I like this method because it is a little bit realistic. Some people might not like using percentile dice to work out the digits. In that case you'd need to assign probabilities using multiple 6 sided dice added together on a bell curve. This would entail a bit more work.