MT does as well...
Note, I am not against have three or more different "gravetic" devices.
Last edited:
What is the climb rate of a Air/Raft?
- Thread starter infojunky
- Start date
Note, I am not against have three or more different "gravetic" devices.
Please note I started this topic after doing similar calculations, coming to the same conclusions.
One of the issues I keep running into is what Altitude orbit is considered to be.
As the written in Book3, it appears there is a drop off of performance as distance increases, using the RAW. But I don't have an issue with that as in other places in CT sans Striker Air/rafts have at best very limited performance away from a planet. (Heck reading Striker, "Anti-gravity is the second major breakthrough. The postulated technology produces both neutralization of weight and lateral thrust. Striker book3. pg. 5". There is more going on than just brute thrust).
Spinward Flow
SOC-14 5K
There undoubtedly is ... but it's hard to look at the rather obvious "physics lessons" in LBB2 (including vector math for movement!) and even more extensively documented in LBB6 and come away with anything akin to the "gamer simpleton" mindset that Traveller is in the habit of "switching off inconveniences of the universe" in order to nullify them in order to make problems (magically) just GO AWAY.
LBB2 and LBB6 respect real world physics enough to include formulas to calculate all kinds of things rather accurately, rather than just handwaving them away.
AnotherDilbert
SOC-14 1K
An orbit is basically an energy state ≈ velocity + potential energy, not distance.
https://en.wikipedia.org/wiki/Low_Earth_orbit
Once in orbit, the spacecraft rotates quickly enough around the planet to make lateral distance meaningless.
Having quite recently spent 11 hours in the center seat of the center row of a 787... let's just say I have a slightly changed perspective on how pleasant an "Hours= UWP Size Code" trip to orbit in cramped conditions might be. (And that's with being able to walk the aisle, and NOT in a vacc suit...)
LBB3 Speeder was subsonic.Now it MAY be possible to reach Mach 1 with that or throw on a vacc suit and haul a ton of cargo to orbit standing on THAT, but I would not be the guy to test that flight envelope.
Air/raft was drag-limited.
I've done the math herw before, and the getting up to near-vacuum altitude makes it only really useful on long trips -- but it can be a significant advantage for those.
Spinward Flow
SOC-14 5K
Actually, the LBB3 Speeder was transonic (1200kph max) rather than subsonic (800kph max).
Great minds think alike.
kilemall
SOC-14 5K
Sorry for your loss.Great minds think alike.
Ummm … 2G thrust - 1G gravity = 1.7G acceleration?
Vectors and Gravity and Pythagoras, oh my!
Imagine a rocket (traditional CHEMICAL rocket for a moment) with a constant thrust of 2G.
Point this rocket up at some angle represented by the hypotenuse of a right triangle.
The Hypotenuse represents the 2G thrust vector of the rocket and is 2 “units” long.
The vertical side of the triangle represents EVIL GRAVITY pulling our heroic rocket back to earth at 1G, so it is a vector 1 “unit” long.
The horizontal side of the triangle represents the resulting vector that our heroic rocket will actually accelerate.
What is the length of the horizontal vector?
Pythagoras … a^2 + b^2 = c^2 … a^2 + 1^2 = 2^2
a^2 = 2^2 - 1^2 = 4-1 = 3
a = sqrt (3) = 1.7321 G
Our heroic rocket with 2G thrust can accelerate 1G straight UP if it wanted to … or it could accelerate 1.7321 G horizontally instead.
Weird, huh?
So a 1G rocket on a 0.9 G world = 0.1G vertical OR sqrt (1^2 - 0.9^2) = 0.435 G horizontal.
Either way, you need to accelerate to meet the delta-v budget needed to reach Low orbit where you are no longer thrusting against gravity (By achieving orbital velocity at orbital altitude).
Vectors and Gravity and Pythagoras, oh my!
Imagine a rocket (traditional CHEMICAL rocket for a moment) with a constant thrust of 2G.
Point this rocket up at some angle represented by the hypotenuse of a right triangle.
The Hypotenuse represents the 2G thrust vector of the rocket and is 2 “units” long.
The vertical side of the triangle represents EVIL GRAVITY pulling our heroic rocket back to earth at 1G, so it is a vector 1 “unit” long.
The horizontal side of the triangle represents the resulting vector that our heroic rocket will actually accelerate.
What is the length of the horizontal vector?
Pythagoras … a^2 + b^2 = c^2 … a^2 + 1^2 = 2^2
a^2 = 2^2 - 1^2 = 4-1 = 3
a = sqrt (3) = 1.7321 G
Our heroic rocket with 2G thrust can accelerate 1G straight UP if it wanted to … or it could accelerate 1.7321 G horizontally instead.
Weird, huh?
So a 1G rocket on a 0.9 G world = 0.1G vertical OR sqrt (1^2 - 0.9^2) = 0.435 G horizontal.
Either way, you need to accelerate to meet the delta-v budget needed to reach Low orbit where you are no longer thrusting against gravity (By achieving orbital velocity at orbital altitude).
Last edited:
Nightwind1
SOC-12
African air/raft or European air/raft?
I see you understood my math and didn't my facetiousness.
Art, you forgot to subtract local gravity... your 45° thrust only gets 0.73-ish g up on a 1g world...
Oh, and the math for reasonable LEO? figure 0.9×GLocal... That's ISS height, per google's top several results, including NASA.
No, I calculated correctly. The ship thrust at 2G at an angle (T/W ratio = 2) and subtracted a 1G downward vector for local gravity. If the hypotenuse is “2” and one side is “1”, what is the length of the other side of the triangle? Vector addition and subtraction is a “Traveller thing”.
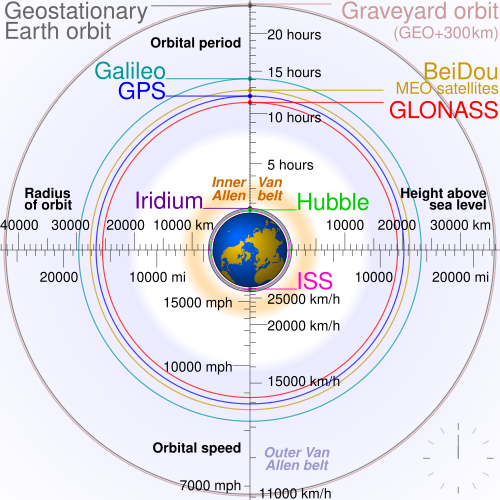
Could you explain that? It seems interesting, but I just don’t follow.
0.9 x GLocal on earth = 0.9 x 1G = 0.9 … 0.9 what?
Spinward Flow
SOC-14 5K
LBB2.81, p36-37.
Specifically the picture on p37 is going to be really helpful in figuring this one out.
Simple answer is that because r2 distance from the center of the planet is "farther away" at LEO than the surface, the gravitational acceleration is lower ... hence 0.9G at the LEO altitude of the ISS, compared to the 1G on the world surface.
Oh, that’s what he was talking about.
g = GM/r^2
G = 6.674E−11 N⋅m2/kg2
M = Mass of Earth = 5.9722E24 kg
r = radius of Earth = 6.3781E6 m
g = Gravity at Surface of Earth = 6.674E−11 x 5.9722E24 / (6.3781E6)^2 = 9.798
At 400km LEO …
g = Gravity at LEO = 6.674E−11 x 5.9722E24 / (6.7781E6)^2 = 8.6757
8.6757 / 9.798 x 100 = 88.545% … OK, so 0.9 G is about correct for LEO.
Much simpler - just use NASA's numbers, which are plenty close for game.
Your 2G air raft needs to use a declining amount of vertical thrust until it hits an orbital speed
your vertical component is (sin(45°)×2g)-GLocalat elevation the sin is roughly 0.7071, and thus the vertical is 1.4142-1 = 0.4142 G vertical at takeoff, and 1.4142-0.9= 0.5142 G vertical at LEO.
Unless you're playing TNE or T4, where gravitics disconnect gravitic from inertial mass, in which case, you've got 1.400 G vertical..
Thrust vertical always reduces by applied gravity. Real world, there's no evidence for a disconnect between inertial mass and gravitic mass. But in TNE, turn on the contragrav, and for gravity purposes your mass is 2% or less of the mass you have to accelerate.
Keep in mind as well - this will affect falling speeds and impact damage, too...
